| ||||
| AVANCES| Modelos de fractales aplicables a la naturaleza | ||||
|
Los modelos de reacción-difusión se utilizan con frecuencia para describir fenómenos de propagación (tales como invasiones biológicas a través de territorios, propagación del fuego en incendios forestales, propagación de epidemias, etc.). Sin embargo, estos modelos tienen la limitación de que suelen considerar que el espacio a lo largo del cual tiene lugar la propagación es homogéneo, mientras que la experiencia nos dice que los espacios físicos presentan formas mucho más complicadas, con gran cantidad de obstáculos y heterogeneidades que limitan el avance de los individuos (o partículas). Con el objetivo
de reparar este problema, en nuestro trabajo hemos tratado de
aplicar la reacción-difusión a la propagación de individuos en los
llamados medios fractales. Los fractales son estructuras que
presentan una propiedad conocida como autosimilitud, que significa
básicamente que vistas a diferentes escalas son iguales. Así, por
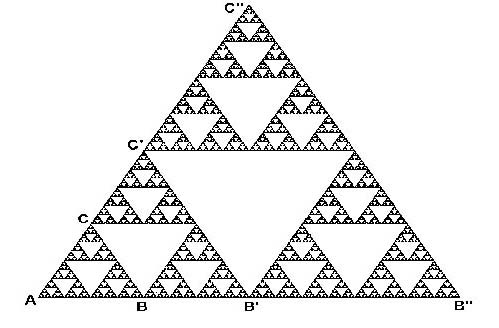
ejemplo, en el dibujo se puede observar que el triángulo ABC es
igual al triángulo AB'C' (e igual al AB"C") sólo que a una escala
más pequeña. Esta figura corresponde a uno de los fractales más
conocidos, el Sierpinski Gasket. A pesar de que puedan parecer a simple vista artificiales, estas estructuras son de gran interés debido a que muchas estructuras de la naturaleza presentan también esta propiedad de la autosimilitud. Ejemplos de ello son el contorno de las costas de un país, las redes hidrográficas o redes de carreteras de un territorio, las ramificaciones de los árboles... y así una infinidad de casos. Si uno pretende explicar un proceso de transporte en estructuras como el Sierpinski Gasket, el principal inconveniente estriba en que no todos los puntos de la estructura están conectados de la misma manera (no son equivalentes), lo que obliga a trabajar con relaciones de tipo estadístico. En nuestro caso hemos ideado lo que podemos llamar el método de las dos escalas, que consiste en observar que las relaciones entre los puntos de la estructura son diferentes a distancias pequeñas o grandes. En las escalas
más pequeñas, vemos que el Sierpinski está formado por pequeños
triángulos, todos ellos iguales; así, se puede decir que a escala
pequeña todos los puntos sí son equivalentes. Cuando uno combina ambas cosas (equivalencia de los puntos a escala pequeña y dominancia de la autosimilitud a escalas mayores), se puede llegar a determinar la forma exacta de los parámetros de transporte y por tanto formular un modelo matemático analítico capaz de describir el proceso. Así, la mayor parte de sistemas donde aparece un transporte a través de medios autosimilares (dispersión de contaminantes a través de ríos, la conducción de nutrientes en los árboles, etc.) se convierten en aplicaciones potenciales de nuestro modelo. Actualmente tratamos de aplicar el modelo a algunos de estos casos prácticos para determinar su validez. Daniel Campos
Moreno |
 | |||
| Universitat Autònoma de Barcelona Àrea de Comunicació i de Promoció Edifici A 08193 Bellaterra (Cerdanyola del Vallès) Tel.: +34 93 581 33 01 | ||||
| premsa.ciencia@uab.es | ||||